
■まさかこんなことしていませんよね
データを集めて下限値を設定するときどうしていますか?
まさか
\[\bar x-\kappa\hat\sigma\,(\kappa は定数) \tag{mis-1}\]
を下限値にしていないですよね。
これは論外です。
統計学をかじったことのある人は,「そんな愚かなことはしてないよ,ちゃんと
\[\bar x-\kappa\left(1+\frac{1}{\sqrt{n}}\right)\hat\sigma \tag{mis-2}\]
としてるよ」と言うかもしれません。
しかし,これも五十歩百歩です。
これらを下限値として設計したあなたの製品は,思わぬところで故障や事故を起こし,最悪の場合は業務上過失で訴えられるかもしれません。
■では,どうするのが正しいのか?
片側許容限界を使います。
実際に,大手のメーカーではちゃんと統計学の専門家を置いて,そんな愚かな設計はしないようにしていますので,安心して製品をお使いください。
(私は決して大手のメーカーの回し者ではないので,誤解のないように。。。)
集めたデータから求めた不偏平均 \(\bar x\) や不偏標準偏差 \(\hat\sigma\) は,あくまで母数の推定値です。
したがって,不偏平均 \(\bar x\) と母平均 \(\mu\) との間にはずれが生じています。
また,不偏標準偏差 \(\hat\sigma\) と母標準偏差 \(\sigma\) もずれています。
母数が真の値だと考えると,それらのずれを考慮せずに設定した下限値は過小評価(真の下限値より高い値)になってしまいます。
式(mis-1)は平均のずれも標準偏差のずれも考慮できていません。
すなわち,不偏平均も不偏標準偏差も真の値だと考えています。
式(mis-2)は,平均のずれは考慮しているものの,不偏標準偏差を真の標準偏差だとしてしまっています。
片側許容限界は,平均と標準偏差,両方のずれを考慮した上で下限値を設定します。
なお,上限値を設定するときも同様です。
片側許容限界では,上側限界値は \(\bar x+k\,\hat\sigma\),下側限界値は \(\bar x-k\,\hat\sigma\) で与えます
( \(k\) は冒頭の \(\kappa\) とは異なります)
。
\(k\) は上側限界値も下側限界値も同じ値です。
なぜなら,データのばらつきは正規分布に従っているという大前提があるからです。
データのばらつきが正規分布に従わないということが予め分かっているときは,特別な処理が必要です。
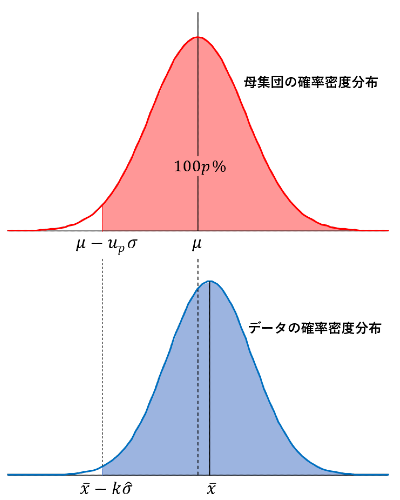
母集団の平均を \(\mu\),分散を \(\sigma^2\) とし,母集団の \(100p\,\%\) のデータを含む下側限界値を \(\mu-u_p\,\sigma\) と表します
( \(u_p\) は冒頭の \(\kappa\) に相当します)
。
一方,標本の平均を \(\bar x\),不偏分散を \(\hat\sigma^2\) とすると,母集団と標本の確率密度分布の関係は図のようになります。
推定による誤差が存在しますので,\(\bar x\ne\mu,\,\hat\sigma\ne\sigma\) です。
ここで,\(\bar x-k\,\hat\sigma\) が母集団の下側限界値を下回る確率を \(\gamma\) とすると,
\[
P_r[\,\bar x-k\hat\sigma\le\mu-u_p\,\sigma\,]=\gamma
\tag{1}
\]
と書くことができます。
ただし,\(P_r[X]\) は事象 \(X\) の発生確率を表す記号です。
\(1-\gamma\) は \(\bar x-k\,\hat\sigma\) が母集団の下側限界値を下回ってしまう危険を犯す確率,すなわち危険率ですので,\(\gamma\) は \(\bar x-k\hat\sigma=\mu-u_p\,\sigma\) と置くことに対する信頼水準となります。
この考え方は,今は高校数学Bで習うようですね。
式(1)を変形して,
\begin{eqnarray}
P_r\left[\,\bar x-k\hat\sigma\le\mu-u_p\,\sigma\,\right]
&=&P_r\left[\,\bar x-\mu+u_p\,\sigma\le k\hat\sigma\,\right]\\
&=&P_r\left[\,\frac{\bar x-\mu+u_p\,\sigma}{\hat\sigma}\le k\,\right]\\
&=&P_r\left[\,\frac{\displaystyle{\frac{\bar x-\mu}{\sigma /\sqrt{n}}+u_p\sqrt{n}}}{\sqrt{\displaystyle{\frac{\hat\sigma^2}{\sigma^2}}}}\le k\sqrt{n}\,\right]=\gamma
\tag{2}
\end{eqnarray}
となります。
ここで,
\(z=\displaystyle{\frac{\bar x-\mu}{\sigma/\sqrt{n}}}\)
は標準正規分布,
\(\chi^2=(n-\delta)\displaystyle{\frac{\hat\sigma^2}{\sigma^2}}\)
は自由度 \(n-\delta\) のカイ二乗分布に従う変数です。
ただし,\(\delta\) は不偏分散 \(\hat\sigma^2\) を計算したときに失った自由度です。(これは大学教養レベルの統計学の基礎です)
これらの分布が既知の変数を使って,式(2)は
\[
P_r\left[\,\frac{z+u_p\sqrt{n}}{\sqrt{\chi^2/(n-\delta)}}\le k\sqrt{n}\,\right]=\gamma
\tag{3}
\]
と表すことができます。
ここで,
\(t'=\displaystyle{\frac{z+\lambda}{\sqrt{\chi^2/\nu}}}\)
という新しい変数を導入します。
この変数は,自由度 \(\nu\) ,非心度 \(\lambda\) の非心t分布という分布関数に従います。(これは大学専門レベル)
この変数を使うと,式(3)は
\[
P_r\left[\,t'\le k\sqrt{n}\,\right]=\gamma
\tag{4}
\]
と書くことができます。
ただし,\(\nu=n-\delta\,,\,\lambda=u_p\sqrt{n}\) です。
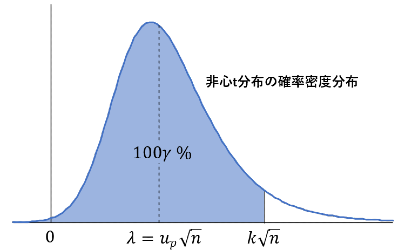
式(4)は,自由度 \(n-\delta\),非心度 \(u_p\sqrt{n}\) の非心t分布の累積確率が \(\gamma\) となる点が \(k\sqrt{n}\) であることを表しています。
したがって,非心t分布の逆関数から \(k\) を得ることができます。
非心t分布の累積分布関数を \(F(t')\) ,逆関数を \(F^{-1}(\gamma)\) と書くと,
\[
k=\frac{F^{-1}(\gamma)}{\sqrt{n}}
\tag{5}
\]
となります。
残念ながらExcelには非心t分布を計算できる関数が用意されていません。 仕方がないので,Excelマクロでユーザ定義関数を作りました。 以下からダウンロードできます。
中身はExcelアドインとマニュアル(PDF)です。 アドインのファイル名は "非心t分布.xlam" です。 ダウンロードしたマクロを使用するのに抵抗がある人は,以下にVBAのソースを公開しておきますので,ご自分でExcelに組み込んでください。 また,マニュアルは こちら から閲覧できます。
非心カイ二乗分布と非心F分布のExcelアドインも作成しています。 欲しい人は "Sainokawa" のページからご連絡ください。
信頼水準 \(\gamma\) の下で \(100p\,\%\) のデータを含む片側限界値の係数 \(k\) を,Excelで求める手順を以下に説明します。 \(n\) は標本サイズです。
以上を1つの数式で書くと,\(k\) は
=t_Inv_Nc( \(\gamma\) , \(n-\delta\) ,NORM.S.INV( \(p\) )*SQRT( \(n\) ))/SQRT( \(n\) )
となります。